Project 3: Implement SLAM¶
Project Overview¶
In this project, you'll implement SLAM for robot that moves and senses in a 2 dimensional, grid world!
SLAM gives us a way to both localize a robot and build up a map of its environment as a robot moves and senses in real-time. This is an active area of research in the fields of robotics and autonomous systems. Since this localization and map-building relies on the visual sensing of landmarks, this is a computer vision problem.
Using what you've learned about robot motion, representations of uncertainty in motion and sensing, and localization techniques, you will be tasked with defining a function, slam, which takes in six parameters as input and returns the vector mu.
mucontains the (x,y) coordinate locations of the robot as it moves, and the positions of landmarks that it senses in the world
You can implement helper functions as you see fit, but your function must return mu. The vector, mu, should have (x, y) coordinates interlaced, for example, if there were 2 poses and 2 landmarks, mu will look like the following, where P is the robot position and L the landmark position:
mu = matrix([[Px0],
[Py0],
[Px1],
[Py1],
[Lx0],
[Ly0],
[Lx1],
[Ly1]])
You can see that mu holds the poses first (x0, y0), (x1, y1), ..., then the landmark locations at the end of the matrix; we consider a nx1 matrix to be a vector.
Generating an environment¶
In a real SLAM problem, you may be given a map that contains information about landmark locations, and in this example, we will make our own data using the make_data function, which generates a world grid with landmarks in it and then generates data by placing a robot in that world and moving and sensing over some numer of time steps. The make_data function relies on a correct implementation of robot move/sense functions, which, at this point, should be complete and in the robot_class.py file. The data is collected as an instantiated robot moves and senses in a world. Your SLAM function will take in this data as input. So, let's first create this data and explore how it represents the movement and sensor measurements that our robot takes.
Create the world¶
Use the code below to generate a world of a specified size with randomly generated landmark locations. You can change these parameters and see how your implementation of SLAM responds!
data holds the sensors measurements and motion of your robot over time. It stores the measurements as data[i][0] and the motion as data[i][1].
Helper functions¶
You will be working with the robot class that may look familiar from the first notebook,
In fact, in the helpers.py file, you can read the details of how data is made with the make_data function. It should look very similar to the robot move/sense cycle you've seen in the first notebook.
In [124]:
Copied!
import numpy as np
from helpers import make_data
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 40.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data, robot = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
import numpy as np
from helpers import make_data
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 40.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data, robot = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
Landmarks: [[18, 89], [69, 87], [90, 4], [50, 26], [62, 51]] Robot: [x=82.09985 y=4.82303]
In [125]:
Copied!
robot.path
robot.path
Out[125]:
[[50.0, 50.0], [47.9653139108604, 70.87161995162137], [46.66831802984643, 90.10390099865566], [64.9704446366091, 77.4106448190126], [80.17310381101771, 64.23715998766768], [94.91763548457514, 53.502443213027924], [77.08680761056024, 40.73509636452328], [59.702645485723146, 30.275962929087015], [41.70453017836984, 20.06209885054181], [25.45398739107488, 8.48256679673503], [30.570711182198295, 28.194910946997087], [36.607433722001275, 46.682605230459274], [42.920363188234894, 65.51438580614918], [48.20551574003593, 86.66781862781585], [29.903323916004695, 93.60054185900569], [39.160937351731135, 76.84657271867609], [50.538242710815986, 60.96459525262081], [60.09765529394042, 41.61714396696874], [70.6945585558651, 22.544039120924644], [82.09984637157041, 4.823028844244325]]
A note on make_data¶
The function above, make_data, takes in so many world and robot motion/sensor parameters because it is responsible for:
- Instantiating a robot (using the robot class)
- Creating a grid world with landmarks in it
This function also prints out the true location of landmarks and the final robot location, which you should refer back to when you test your implementation of SLAM.
The data this returns is an array that holds information about robot sensor measurements and robot motion (dx, dy) that is collected over a number of time steps, N. You will have to use only these readings about motion and measurements to track a robot over time and find the determine the location of the landmarks using SLAM. We only print out the true landmark locations for comparison, later.
In data the measurement and motion data can be accessed from the first and second index in the columns of the data array. See the following code for an example, where i is the time step:
measurement = data[i][0]
motion = data[i][1]
In [126]:
Copied!
# print out some stats about the data
time_step = 0
print('Example measurements: \n', data[time_step][0])
print('\n')
print('Example motion: \n', data[time_step][1])
# print out some stats about the data
time_step = 0
print('Example measurements: \n', data[time_step][0])
print('\n')
print('Example motion: \n', data[time_step][1])
Example measurements: [[0, -32.09960529315943, 39.66833246766444], [1, 19.586368844525015, 35.85549304306623], [3, 1.531243254884402, -22.343892559365603], [4, 13.90407402915669, 1.5378339984084413]] Example motion: [-0.3757560909009105, 19.99646987245876]
Try changing the value of time_step, you should see that the list of measurements varies based on what in the world the robot sees after it moves. As you know from the first notebook, the robot can only sense so far and with a certain amount of accuracy in the measure of distance between its location and the location of landmarks. The motion of the robot always is a vector with two values: one for x and one for y displacement. This structure will be useful to keep in mind as you traverse this data in your implementation of slam.
Initialize Constraints¶
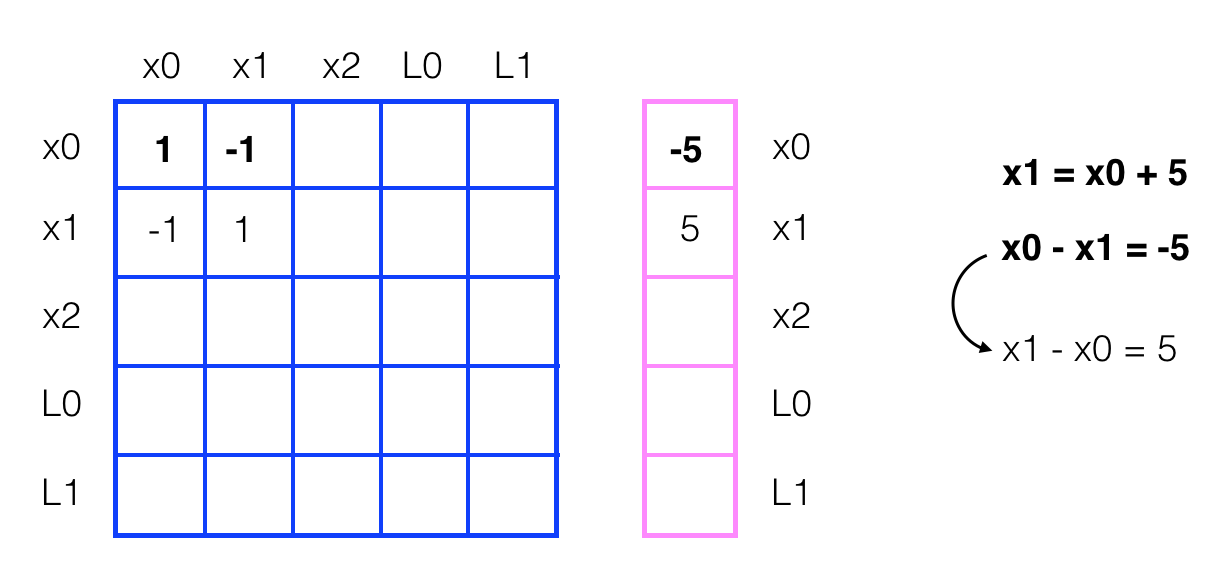
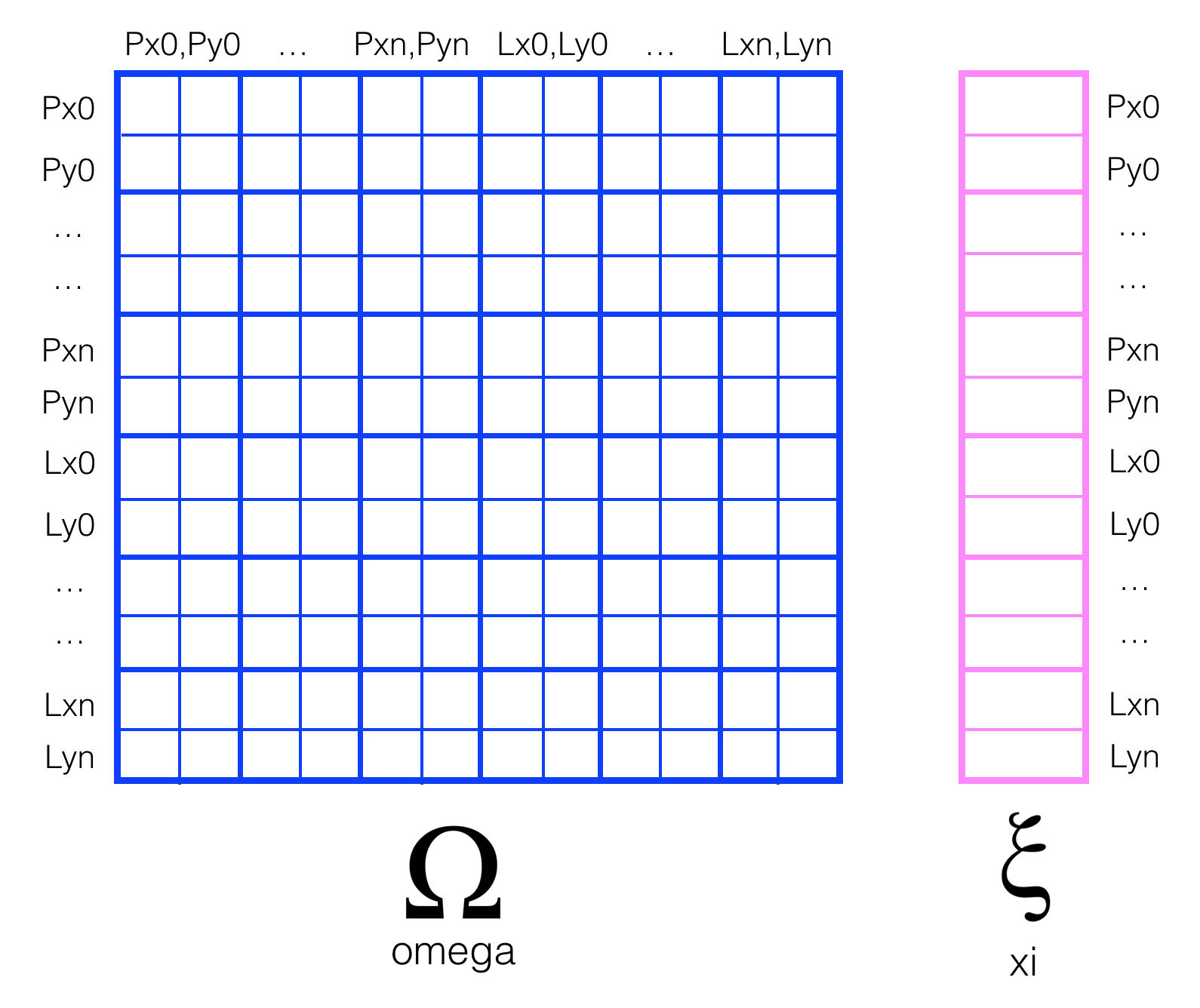
One of the most challenging tasks here will be to create and modify the constraint matrix and vector: omega and xi. In the second notebook, you saw an example of how omega and xi could hold all the values that define the relationships between robot poses xi and landmark positions Li in a 1D world, as seen below, where omega is the blue matrix and xi is the pink vector.
In this project, you are tasked with implementing constraints for a 2D world. We are referring to robot poses as Px, Py and landmark positions as Lx, Ly, and one way to approach this challenge is to add both x and y locations in the constraint matrices.
You may also choose to create two of each omega and xi (one for x and one for y positions).
TODO: Write a function that initializes omega and xi¶
Complete the function initialize_constraints so that it returns omega and xi constraints for the starting position of the robot. Any values that we do not yet know should be initialized with the value 0. You may assume that our robot starts out in exactly the middle of the world with 100% confidence (no motion or measurement noise at this point). The inputs N time steps, num_landmarks, and world_size should give you all the information you need to construct intial constraints of the correct size and starting values.
Depending on your approach you may choose to return one omega and one xi that hold all (x,y) positions *or two of each (one for x values and one for y); choose whichever makes most sense to you!*
In [127]:
Copied!
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
omega = [0]
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = [0]
# initialize constraint matrices with 0's
# Now these are 4x4 because of 3 poses and a landmark
size = 2*N + 2*num_landmarks
omega = np.zeros((size, size))
xi = np.zeros((size, 1))
# add initial pose constraint
omega[0][0] = 1
omega[1][1] = 1
xi[0] = world_size/2
xi[1] = world_size/2
return omega, xi
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
omega = [0]
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = [0]
# initialize constraint matrices with 0's
# Now these are 4x4 because of 3 poses and a landmark
size = 2*N + 2*num_landmarks
omega = np.zeros((size, size))
xi = np.zeros((size, 1))
# add initial pose constraint
omega[0][0] = 1
omega[1][1] = 1
xi[0] = world_size/2
xi[1] = world_size/2
return omega, xi
Test as you go¶
It's good practice to test out your code, as you go. Since slam relies on creating and updating constraint matrices, omega and xi to account for robot sensor measurements and motion, let's check that they initialize as expected for any given parameters.
Below, you'll find some test code that allows you to visualize the results of your function initialize_constraints. We are using the seaborn library for visualization.
Please change the test values of N, landmarks, and world_size and see the results. Be careful not to use these values as input into your final slam function.
This code assumes that you have created one of each constraint: omega and xi, but you can change and add to this code, accordingly. The constraints should vary in size with the number of time steps and landmarks as these values affect the number of poses a robot will take (Px0,Py0,...Pxn,Pyn) and landmark locations (Lx0,Ly0,...Lxn,Lyn) whose relationships should be tracked in the constraint matrices. Recall that omega holds the weights of each variable and xi holds the value of the sum of these variables, as seen in Notebook 2. You'll need the world_size to determine the starting pose of the robot in the world and fill in the initial values for xi.
In [128]:
Copied!
#%matplotlib notebook
#%matplotlib notebook
In [129]:
Copied!
# import data viz resources
import matplotlib.pyplot as plt
from pandas import DataFrame
import seaborn as sns
%matplotlib inline
# import data viz resources
import matplotlib.pyplot as plt
from pandas import DataFrame
import seaborn as sns
%matplotlib inline
In [130]:
Copied!
# define a small N and world_size (small for ease of visualization)
N_test = 5
num_landmarks_test = 2
small_world = 10
# initialize the constraints
initial_omega, initial_xi = initialize_constraints(N_test, num_landmarks_test, small_world)
# define a small N and world_size (small for ease of visualization)
N_test = 5
num_landmarks_test = 2
small_world = 10
# initialize the constraints
initial_omega, initial_xi = initialize_constraints(N_test, num_landmarks_test, small_world)
In [131]:
Copied!
# define figure size
plt.rcParams["figure.figsize"] = (10,7)
# display omega
sns.heatmap(DataFrame(initial_omega), cmap='Blues', annot=True, linewidths=.5)
# define figure size
plt.rcParams["figure.figsize"] = (10,7)
# display omega
sns.heatmap(DataFrame(initial_omega), cmap='Blues', annot=True, linewidths=.5)
Out[131]:
<matplotlib.axes._subplots.AxesSubplot at 0x7fef941b9c88>
In [132]:
Copied!
# define figure size
plt.rcParams["figure.figsize"] = (1,7)
# display xi
sns.heatmap(DataFrame(initial_xi), cmap='Oranges', annot=True, linewidths=.5)
# define figure size
plt.rcParams["figure.figsize"] = (1,7)
# display xi
sns.heatmap(DataFrame(initial_xi), cmap='Oranges', annot=True, linewidths=.5)
Out[132]:
<matplotlib.axes._subplots.AxesSubplot at 0x7fef8fbba630>
SLAM inputs¶
In addition to data, your slam function will also take in:
- N - The number of time steps that a robot will be moving and sensing
- num_landmarks - The number of landmarks in the world
- world_size - The size (w/h) of your world
- motion_noise - The noise associated with motion; the update confidence for motion should be
1.0/motion_noise - measurement_noise - The noise associated with measurement/sensing; the update weight for measurement should be
1.0/measurement_noise
A note on noise¶
Recall that omega holds the relative "strengths" or weights for each position variable, and you can update these weights by accessing the correct index in omega omega[row][col] and adding/subtracting 1.0/noise where noise is measurement or motion noise. Xi holds actual position values, and so to update xi you'll do a similar addition process only using the actual value of a motion or measurement. So for a vector index xi[row][0] you will end up adding/subtracting one measurement or motion divided by their respective noise.
TODO: Implement Graph SLAM¶
Follow the TODO's below to help you complete this slam implementation (these TODO's are in the recommended order), then test out your implementation!
Updating with motion and measurements¶
With a 2D omega and xi structure as shown above (in earlier cells), you'll have to be mindful about how you update the values in these constraint matrices to account for motion and measurement constraints in the x and y directions. Recall that the solution to these matrices (which holds all values for robot poses P and landmark locations L) is the vector, mu, which can be computed at the end of the construction of omega and xi as the inverse of omega times xi: $\mu = \Omega^{-1}\xi$
You may also choose to return the values of omega and xi if you want to visualize their final state!
In [133]:
Copied!
def plot_omega(omega):
# define figure size
plt.figure()
plt.rcParams["figure.figsize"] = (20,14)
# display omega
sns.heatmap(DataFrame(omega), cmap='Blues', annot=True, linewidths=.5)
def plot_xi(xi):
# define figure size
plt.figure()
plt.rcParams["figure.figsize"] = (1,14)
# display xi
sns.heatmap(DataFrame(xi), cmap='Oranges', annot=True, linewidths=.5)
def plot_omega(omega):
# define figure size
plt.figure()
plt.rcParams["figure.figsize"] = (20,14)
# display omega
sns.heatmap(DataFrame(omega), cmap='Blues', annot=True, linewidths=.5)
def plot_xi(xi):
# define figure size
plt.figure()
plt.rcParams["figure.figsize"] = (1,14)
# display xi
sns.heatmap(DataFrame(xi), cmap='Oranges', annot=True, linewidths=.5)
In [134]:
Copied!
def construct_constraints_sense(N, num_landmarks, time_step, measurement, measurement_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific measurement including its noise,
and returns constraint matrices, omega and xi.'''
size = 2 * (N + num_landmarks)
landmark_index = measurement[0]
dx = measurement[1]
dy = measurement[2]
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# initialize constraint matrices with 0's
omega = np.zeros((size, size))
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((size, 1))
strength = 1.0 / measurement_noise
# incorporate sense constraint for x coordinate
x_idx = time_step*2
lx_idx = 2 * (N + landmark_index)
omega[x_idx][x_idx] = strength
omega[x_idx][lx_idx] = -strength
omega[lx_idx][x_idx] = -strength
omega[lx_idx][lx_idx] = strength
xi[x_idx] = -dx / measurement_noise
xi[lx_idx] = dx / measurement_noise
# incorporate sense constraint for y coordinate
y_idx = time_step*2 + 1
ly_idx = 2 * (N + landmark_index) + 1
omega[y_idx][y_idx] = strength
omega[y_idx][ly_idx] = -strength
omega[ly_idx][y_idx] = -strength
omega[ly_idx][ly_idx] = strength
xi[y_idx] = -dy / measurement_noise
xi[ly_idx] = dy / measurement_noise
return omega, xi
def construct_constraints_sense(N, num_landmarks, time_step, measurement, measurement_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific measurement including its noise,
and returns constraint matrices, omega and xi.'''
size = 2 * (N + num_landmarks)
landmark_index = measurement[0]
dx = measurement[1]
dy = measurement[2]
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# initialize constraint matrices with 0's
omega = np.zeros((size, size))
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((size, 1))
strength = 1.0 / measurement_noise
# incorporate sense constraint for x coordinate
x_idx = time_step*2
lx_idx = 2 * (N + landmark_index)
omega[x_idx][x_idx] = strength
omega[x_idx][lx_idx] = -strength
omega[lx_idx][x_idx] = -strength
omega[lx_idx][lx_idx] = strength
xi[x_idx] = -dx / measurement_noise
xi[lx_idx] = dx / measurement_noise
# incorporate sense constraint for y coordinate
y_idx = time_step*2 + 1
ly_idx = 2 * (N + landmark_index) + 1
omega[y_idx][y_idx] = strength
omega[y_idx][ly_idx] = -strength
omega[ly_idx][y_idx] = -strength
omega[ly_idx][ly_idx] = strength
xi[y_idx] = -dy / measurement_noise
xi[ly_idx] = dy / measurement_noise
return omega, xi
In [135]:
Copied!
def construct_constraints_move(N, num_landmarks, time_step, motion, motion_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific motion including its noise,
and returns constraint matrices, omega and xi.'''
size = 2 * (N + num_landmarks)
dx = motion[0]
dy = motion[1]
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# initialize constraint matrices with 0's
omega = np.zeros((size, size))
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((size, 1))
strength = 1.0 / motion_noise
# incorporate motion constraint for x coordinate
x0 = time_step*2
x1 = x0 + 2
omega[x0][x0] = strength
omega[x0][x1] = -strength
omega[x1][x0] = -strength
omega[x1][x1] = strength
xi[x0] = -dx / motion_noise
xi[x1] = dx / motion_noise
# incorporate motion constraint for y coordinate
y0 = time_step*2 + 1
y1 = y0 + 2
omega[y0][y0] = strength
omega[y0][y1] = -strength
omega[y1][y0] = -strength
omega[y1][y1] = strength
xi[y0] = -dy / motion_noise
xi[y1] = dy / motion_noise
return omega, xi
def construct_constraints_move(N, num_landmarks, time_step, motion, motion_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific motion including its noise,
and returns constraint matrices, omega and xi.'''
size = 2 * (N + num_landmarks)
dx = motion[0]
dy = motion[1]
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# initialize constraint matrices with 0's
omega = np.zeros((size, size))
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((size, 1))
strength = 1.0 / motion_noise
# incorporate motion constraint for x coordinate
x0 = time_step*2
x1 = x0 + 2
omega[x0][x0] = strength
omega[x0][x1] = -strength
omega[x1][x0] = -strength
omega[x1][x1] = strength
xi[x0] = -dx / motion_noise
xi[x1] = dx / motion_noise
# incorporate motion constraint for y coordinate
y0 = time_step*2 + 1
y1 = y0 + 2
omega[y0][y0] = strength
omega[y0][y1] = -strength
omega[y1][y0] = -strength
omega[y1][y1] = strength
xi[y0] = -dy / motion_noise
xi[y1] = dy / motion_noise
return omega, xi
In [136]:
Copied!
## TODO: Complete the code to implement SLAM
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
omega, xi = initialize_constraints(N, num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
for time_step in range(N-1):
#print(time_step)
measurements = data[time_step][0]
motion = data[time_step][1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measurement in measurements:
omega_sense, xi_sense = construct_constraints_sense(N, num_landmarks, time_step, measurement, measurement_noise)
omega += omega_sense
xi += xi_sense
#plot_omega(omega)
#plot_xi(xi)
#return
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
omega_move, xi_move = construct_constraints_move(N, num_landmarks, time_step, motion, motion_noise)
omega += omega_move
xi += xi_move
#plot_omega(omega)
#plot_xi(xi)
#return
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = None
#plot_omega(omega)
#plot_xi(xi)
#return
omega_inv = np.linalg.inv(np.matrix(omega))
mu = omega_inv*xi
return mu # return `mu`
## TODO: Complete the code to implement SLAM
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
omega, xi = initialize_constraints(N, num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
for time_step in range(N-1):
#print(time_step)
measurements = data[time_step][0]
motion = data[time_step][1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measurement in measurements:
omega_sense, xi_sense = construct_constraints_sense(N, num_landmarks, time_step, measurement, measurement_noise)
omega += omega_sense
xi += xi_sense
#plot_omega(omega)
#plot_xi(xi)
#return
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
omega_move, xi_move = construct_constraints_move(N, num_landmarks, time_step, motion, motion_noise)
omega += omega_move
xi += xi_move
#plot_omega(omega)
#plot_xi(xi)
#return
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = None
#plot_omega(omega)
#plot_xi(xi)
#return
omega_inv = np.linalg.inv(np.matrix(omega))
mu = omega_inv*xi
return mu # return `mu`
Helper functions¶
To check that your implementation of SLAM works for various inputs, we have provided two helper functions that will help display the estimated pose and landmark locations that your function has produced. First, given a result mu and number of time steps, N, we define a function that extracts the poses and landmarks locations and returns those as their own, separate lists.
Then, we define a function that nicely print out these lists; both of these we will call, in the next step.
In [137]:
Copied!
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_poses_landmarks(mu, N):
# create a list of poses
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# create a list of landmarks
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return poses, landmarks
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_poses_landmarks(mu, N):
# create a list of poses
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# create a list of landmarks
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return poses, landmarks
In [138]:
Copied!
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
In [139]:
Copied!
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_pose_landmarks_online(mu):
# create a list of poses
pose = (mu[0].item(), mu[1].item())
# create a list of landmarks
landmarks = []
N = 1
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return pose, landmarks
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_pose_landmarks_online(mu):
# create a list of poses
pose = (mu[0].item(), mu[1].item())
# create a list of landmarks
landmarks = []
N = 1
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return pose, landmarks
In [140]:
Copied!
def print_all_online(pose, landmarks):
print('\n')
print('Estimated Pose:')
print('['+', '.join('%.3f'%p for p in pose)+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
def print_all_online(pose, landmarks):
print('\n')
print('Estimated Pose:')
print('['+', '.join('%.3f'%p for p in pose)+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
Run SLAM¶
Once you've completed your implementation of slam, see what mu it returns for different world sizes and different landmarks!
What to Expect¶
The data that is generated is random, but you did specify the number, N, or time steps that the robot was expected to move and the num_landmarks in the world (which your implementation of slam should see and estimate a position for. Your robot should also start with an estimated pose in the very center of your square world, whose size is defined by world_size.
With these values in mind, you should expect to see a result that displays two lists:
- Estimated poses, a list of (x, y) pairs that is exactly
Nin length since this is how many motions your robot has taken. The very first pose should be the center of your world, i.e.[50.000, 50.000]for a world that is 100.0 in square size. - Estimated landmarks, a list of landmark positions (x, y) that is exactly
num_landmarksin length.
Landmark Locations¶
If you refer back to the printout of exact landmark locations when this data was created, you should see values that are very similar to those coordinates, but not quite (since slam must account for noise in motion and measurement).
In [141]:
Copied!
# call your implementation of slam, passing in the necessary parameters
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
# call your implementation of slam, passing in the necessary parameters
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
Estimated Poses: [50.000, 50.000] [49.438, 70.169] [48.361, 89.863] [64.592, 77.021] [80.771, 64.443] [95.764, 54.027] [78.608, 42.276] [60.960, 30.572] [43.660, 20.198] [26.696, 9.385] [31.650, 28.717] [37.060, 47.409] [43.975, 66.118] [49.716, 86.220] [30.860, 93.758] [40.653, 77.368] [51.684, 60.255] [61.657, 41.688] [72.529, 23.425] [82.204, 5.921] Estimated Landmarks: [18.364, 89.130] [69.980, 86.949] [91.585, 5.242] [51.569, 26.748] [63.195, 51.718]
Visualize the constructed world¶
Finally, using the display_world code from the helpers.py file (which was also used in the first notebook), we can actually visualize what you have coded with slam: the final position of the robot and the positon of landmarks, created from only motion and measurement data!
Note that these should be very similar to the printed true landmark locations and final pose from our call to make_data early in this notebook.
In [142]:
Copied!
# import the helper function
from helpers import display_world, display_world_extended
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
print('True last pose: ', robot.path[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
display_world_extended(int(world_size), poses[-1], landmarks, robot)
# import the helper function
from helpers import display_world, display_world_extended
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
print('True last pose: ', robot.path[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
display_world_extended(int(world_size), poses[-1], landmarks, robot)
Last pose: (82.2038611962253, 5.9212434963337515) True last pose: [82.09984637157041, 4.823028844244325]
Question: How far away is your final pose (as estimated by slam) compared to the true final pose? Why do you think these poses are different?¶
You can find the true value of the final pose in one of the first cells where make_data was called. You may also want to look at the true landmark locations and compare them to those that were estimated by slam. Ask yourself: what do you think would happen if we moved and sensed more (increased N)? Or if we had lower/higher noise parameters.
Answer: (Write your answer here.)
The true landmark positions and the final robot pose are compared to their estimated locations in the following pandas dataframes:
Motion and Measurement Noise
For a motion_noise of 2.0 the mean pose error is 0.993865921977
The mean landmark location error is 0.858795754817 with a measurement_noise of 2.0.
For motion_noise=0.2 the mean pose error decreases to 0.0882231486516.
The same is true for the mean landmark location error. It decreases to 0.0773540304092 when the measurement_noise is set to 0.2.
Changing N
Increasing the time steps N doesn't reduce the error between true and estimated poses. The main issue is the measurement and motion noise.
The error increases when N, the number of sense, move cycles is set too small, meaning that the robot is not able to explore the whole world and therefore might miss some of the landmarks.
In [143]:
Copied!
import pandas as pd
import pandas as pd
In [144]:
Copied!
def calculate_errors(dataframe):
errors = []
for index, row in dataframe.iterrows():
gt = row.iloc[0]
est = row.iloc[1]
error = np.sqrt((gt[0] - est[0])**2 + (gt[1] - est[1])**2)
errors.append(error)
return errors
def calculate_errors(dataframe):
errors = []
for index, row in dataframe.iterrows():
gt = row.iloc[0]
est = row.iloc[1]
error = np.sqrt((gt[0] - est[0])**2 + (gt[1] - est[1])**2)
errors.append(error)
return errors
In [145]:
Copied!
df_landmarks = pd.DataFrame(list(zip(robot.landmarks, landmarks)),
columns =['Landmarks (Ground Truth)', 'Landmarks Estimated'])
df_landmarks['error'] = calculate_errors(df_landmarks)
print("Mean landmark location error: ", np.mean(df_landmarks['error']))
df_landmarks
df_landmarks = pd.DataFrame(list(zip(robot.landmarks, landmarks)),
columns =['Landmarks (Ground Truth)', 'Landmarks Estimated'])
df_landmarks['error'] = calculate_errors(df_landmarks)
print("Mean landmark location error: ", np.mean(df_landmarks['error']))
df_landmarks
Mean landmark location error: 1.30282438513
Out[145]:
| Landmarks (Ground Truth) | Landmarks Estimated | error | |
|---|---|---|---|
| 0 | [18, 89] | (18.36405719564165, 89.13010359088983) | 0.386607 |
| 1 | [69, 87] | (69.98045471591945, 86.9493502529124) | 0.981762 |
| 2 | [90, 4] | (91.58546248832768, 5.2416232456900715) | 2.013782 |
| 3 | [50, 26] | (51.56864778209609, 26.747538544008243) | 1.737662 |
| 4 | [62, 51] | (63.19516104206713, 51.71811349575321) | 1.394309 |
In [146]:
Copied!
df_poses = pd.DataFrame(list(zip(robot.path, poses)),
columns = ['Robot Pose (Ground Truth)', 'Robot Pose Estimated'])
df_poses['error'] = calculate_errors(df_poses)
print("Mean pose error: ", np.mean(df_poses['error']))
df_poses
df_poses = pd.DataFrame(list(zip(robot.path, poses)),
columns = ['Robot Pose (Ground Truth)', 'Robot Pose Estimated'])
df_poses['error'] = calculate_errors(df_poses)
print("Mean pose error: ", np.mean(df_poses['error']))
df_poses
Mean pose error: 1.29529591361
Out[146]:
| Robot Pose (Ground Truth) | Robot Pose Estimated | error | |
|---|---|---|---|
| 0 | [50.0, 50.0] | (49.99999999999985, 50.0) | 1.492140e-13 |
| 1 | [47.9653139109, 70.8716199516] | (49.438004008780396, 70.16913093866839) | 1.631658e+00 |
| 2 | [46.6683180298, 90.1039009987] | (48.3613484935135, 89.86262143791677) | 1.710137e+00 |
| 3 | [64.9704446366, 77.410644819] | (64.59171970265324, 77.02139007457875) | 5.430947e-01 |
| 4 | [80.173103811, 64.2371599877] | (80.77088843363241, 64.44260858598707) | 6.321041e-01 |
| 5 | [94.9176354846, 53.502443213] | (95.76385984050381, 54.02656419804629) | 9.953886e-01 |
| 6 | [77.0868076106, 40.7350963645] | (78.60795822841908, 42.276292520391976) | 2.165453e+00 |
| 7 | [59.7026454857, 30.2759629291] | (60.96010682550587, 30.571796497157187) | 1.291792e+00 |
| 8 | [41.7045301784, 20.0620988505] | (43.659700512526946, 20.19836786089933) | 1.959913e+00 |
| 9 | [25.4539873911, 8.48256679674] | (26.696105438280426, 9.38491673983075) | 1.535283e+00 |
| 10 | [30.5707111822, 28.194910947] | (31.649736401802663, 28.716669572468135) | 1.198552e+00 |
| 11 | [36.607433722, 46.6826052305] | (37.05953922912646, 47.409313061464694) | 8.558643e-01 |
| 12 | [42.9203631882, 65.5143858061] | (43.97456034544608, 66.11753269114453) | 1.214544e+00 |
| 13 | [48.20551574, 86.6678186278] | (49.716087470691065, 86.22023305818547) | 1.575487e+00 |
| 14 | [29.903323916, 93.600541859] | (30.8596240555992, 93.75812932878824) | 9.691975e-01 |
| 15 | [39.1609373517, 76.8465727187] | (40.65306530504595, 77.36807311352446) | 1.580635e+00 |
| 16 | [50.5382427108, 60.9645952526] | (51.68415109497511, 60.25454461488866) | 1.348065e+00 |
| 17 | [60.0976552939, 41.617143967] | (61.6569214175812, 41.688277105275304) | 1.560888e+00 |
| 18 | [70.6945585559, 22.5440391209] | (72.5285881581232, 23.425217092011252) | 2.034733e+00 |
| 19 | [82.0998463716, 4.82302884424] | (82.2038611962253, 5.9212434963337515) | 1.103129e+00 |
Testing¶
To confirm that your slam code works before submitting your project, it is suggested that you run it on some test data and cases. A few such cases have been provided for you, in the cells below. When you are ready, uncomment the test cases in the next cells (there are two test cases, total); your output should be close-to or exactly identical to the given results. If there are minor discrepancies it could be a matter of floating point accuracy or in the calculation of the inverse matrix.
Submit your project¶
If you pass these tests, it is a good indication that your project will pass all the specifications in the project rubric. Follow the submission instructions to officially submit!
In [147]:
Copied!
# Here is the data and estimated outputs for test case 1
test_data1 = [[[[1, 19.457599255548065, 23.8387362100849], [2, -13.195807561967236, 11.708840328458608], [3, -30.0954905279171, 15.387879242505843]], [-12.2607279422326, -15.801093326936487]], [[[2, -0.4659930049620491, 28.088559771215664], [4, -17.866382374890936, -16.384904503932]], [-12.2607279422326, -15.801093326936487]], [[[4, -6.202512900833806, -1.823403210274639]], [-12.2607279422326, -15.801093326936487]], [[[4, 7.412136480918645, 15.388585962142429]], [14.008259661173426, 14.274756084260822]], [[[4, -7.526138813444998, -0.4563942429717849]], [14.008259661173426, 14.274756084260822]], [[[2, -6.299793150150058, 29.047830407717623], [4, -21.93551130411791, -13.21956810989039]], [14.008259661173426, 14.274756084260822]], [[[1, 15.796300959032276, 30.65769689694247], [2, -18.64370821983482, 17.380022987031367]], [14.008259661173426, 14.274756084260822]], [[[1, 0.40311325410337906, 14.169429532679855], [2, -35.069349468466235, 2.4945558982439957]], [14.008259661173426, 14.274756084260822]], [[[1, -16.71340983241936, -2.777000269543834]], [-11.006096015782283, 16.699276945166858]], [[[1, -3.611096830835776, -17.954019226763958]], [-19.693482634035977, 3.488085684573048]], [[[1, 18.398273354362416, -22.705102332550947]], [-19.693482634035977, 3.488085684573048]], [[[2, 2.789312482883833, -39.73720193121324]], [12.849049222879723, -15.326510824972983]], [[[1, 21.26897046581808, -10.121029799040915], [2, -11.917698965880655, -23.17711662602097], [3, -31.81167947898398, -16.7985673023331]], [12.849049222879723, -15.326510824972983]], [[[1, 10.48157743234859, 5.692957082575485], [2, -22.31488473554935, -5.389184118551409], [3, -40.81803984305378, -2.4703329790238118]], [12.849049222879723, -15.326510824972983]], [[[0, 10.591050242096598, -39.2051798967113], [1, -3.5675572049297553, 22.849456408289125], [2, -38.39251065320351, 7.288990306029511]], [12.849049222879723, -15.326510824972983]], [[[0, -3.6225556479370766, -25.58006865235512]], [-7.8874682868419965, -18.379005523261092]], [[[0, 1.9784503557879374, -6.5025974151499]], [-7.8874682868419965, -18.379005523261092]], [[[0, 10.050665232782423, 11.026385307998742]], [-17.82919359778298, 9.062000642947142]], [[[0, 26.526838150174818, -0.22563393232425621], [4, -33.70303936886652, 2.880339841013677]], [-17.82919359778298, 9.062000642947142]]]
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1 = slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
poses_1, landmarks_1 = get_poses_landmarks(mu_1, 20)
print_all(poses_1, landmarks_1)
# Here is the data and estimated outputs for test case 1
test_data1 = [[[[1, 19.457599255548065, 23.8387362100849], [2, -13.195807561967236, 11.708840328458608], [3, -30.0954905279171, 15.387879242505843]], [-12.2607279422326, -15.801093326936487]], [[[2, -0.4659930049620491, 28.088559771215664], [4, -17.866382374890936, -16.384904503932]], [-12.2607279422326, -15.801093326936487]], [[[4, -6.202512900833806, -1.823403210274639]], [-12.2607279422326, -15.801093326936487]], [[[4, 7.412136480918645, 15.388585962142429]], [14.008259661173426, 14.274756084260822]], [[[4, -7.526138813444998, -0.4563942429717849]], [14.008259661173426, 14.274756084260822]], [[[2, -6.299793150150058, 29.047830407717623], [4, -21.93551130411791, -13.21956810989039]], [14.008259661173426, 14.274756084260822]], [[[1, 15.796300959032276, 30.65769689694247], [2, -18.64370821983482, 17.380022987031367]], [14.008259661173426, 14.274756084260822]], [[[1, 0.40311325410337906, 14.169429532679855], [2, -35.069349468466235, 2.4945558982439957]], [14.008259661173426, 14.274756084260822]], [[[1, -16.71340983241936, -2.777000269543834]], [-11.006096015782283, 16.699276945166858]], [[[1, -3.611096830835776, -17.954019226763958]], [-19.693482634035977, 3.488085684573048]], [[[1, 18.398273354362416, -22.705102332550947]], [-19.693482634035977, 3.488085684573048]], [[[2, 2.789312482883833, -39.73720193121324]], [12.849049222879723, -15.326510824972983]], [[[1, 21.26897046581808, -10.121029799040915], [2, -11.917698965880655, -23.17711662602097], [3, -31.81167947898398, -16.7985673023331]], [12.849049222879723, -15.326510824972983]], [[[1, 10.48157743234859, 5.692957082575485], [2, -22.31488473554935, -5.389184118551409], [3, -40.81803984305378, -2.4703329790238118]], [12.849049222879723, -15.326510824972983]], [[[0, 10.591050242096598, -39.2051798967113], [1, -3.5675572049297553, 22.849456408289125], [2, -38.39251065320351, 7.288990306029511]], [12.849049222879723, -15.326510824972983]], [[[0, -3.6225556479370766, -25.58006865235512]], [-7.8874682868419965, -18.379005523261092]], [[[0, 1.9784503557879374, -6.5025974151499]], [-7.8874682868419965, -18.379005523261092]], [[[0, 10.050665232782423, 11.026385307998742]], [-17.82919359778298, 9.062000642947142]], [[[0, 26.526838150174818, -0.22563393232425621], [4, -33.70303936886652, 2.880339841013677]], [-17.82919359778298, 9.062000642947142]]]
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1 = slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
poses_1, landmarks_1 = get_poses_landmarks(mu_1, 20)
print_all(poses_1, landmarks_1)
Estimated Poses: [50.000, 50.000] [37.973, 33.652] [26.185, 18.155] [13.745, 2.116] [28.097, 16.783] [42.384, 30.902] [55.831, 44.497] [70.857, 59.699] [85.697, 75.543] [74.011, 92.434] [53.544, 96.454] [34.525, 100.080] [48.623, 83.953] [60.197, 68.107] [73.778, 52.935] [87.132, 38.538] [80.303, 20.508] [72.798, 2.945] [55.245, 13.255] [37.416, 22.317] Estimated Landmarks: [82.956, 13.539] [70.495, 74.141] [36.740, 61.281] [18.698, 66.060] [20.635, 16.875]
In [148]:
Copied!
# Here is the data and estimated outputs for test case 2
test_data2 = [[[[0, 26.543274387283322, -6.262538160312672], [3, 9.937396825799755, -9.128540360867689]], [18.92765331253674, -6.460955043986683]], [[[0, 7.706544739722961, -3.758467215445748], [1, 17.03954411948937, 31.705489938553438], [3, -11.61731288777497, -6.64964096716416]], [18.92765331253674, -6.460955043986683]], [[[0, -12.35130507136378, 2.585119104239249], [1, -2.563534536165313, 38.22159657838369], [3, -26.961236804740935, -0.4802312626141525]], [-11.167066095509824, 16.592065417497455]], [[[0, 1.4138633151721272, -13.912454837810632], [1, 8.087721200818589, 20.51845934354381], [3, -17.091723454402302, -16.521500551709707], [4, -7.414211721400232, 38.09191602674439]], [-11.167066095509824, 16.592065417497455]], [[[0, 12.886743222179561, -28.703968411636318], [1, 21.660953298391387, 3.4912891084614914], [3, -6.401401414569506, -32.321583037341625], [4, 5.034079343639034, 23.102207946092893]], [-11.167066095509824, 16.592065417497455]], [[[1, 31.126317672358578, -10.036784369535214], [2, -38.70878528420893, 7.4987265861424595], [4, 17.977218575473767, 6.150889254289742]], [-6.595520680493778, -18.88118393939265]], [[[1, 41.82460922922086, 7.847527392202475], [3, 15.711709540417502, -30.34633659912818]], [-6.595520680493778, -18.88118393939265]], [[[0, 40.18454208294434, -6.710999804403755], [3, 23.019508919299156, -10.12110867290604]], [-6.595520680493778, -18.88118393939265]], [[[3, 27.18579315312821, 8.067219022708391]], [-6.595520680493778, -18.88118393939265]], [[], [11.492663265706092, 16.36822198838621]], [[[3, 24.57154567653098, 13.461499960708197]], [11.492663265706092, 16.36822198838621]], [[[0, 31.61945290413707, 0.4272295085799329], [3, 16.97392299158991, -5.274596836133088]], [11.492663265706092, 16.36822198838621]], [[[0, 22.407381798735177, -18.03500068379259], [1, 29.642444125196995, 17.3794951934614], [3, 4.7969752441371645, -21.07505361639969], [4, 14.726069092569372, 32.75999422300078]], [11.492663265706092, 16.36822198838621]], [[[0, 10.705527984670137, -34.589764174299596], [1, 18.58772336795603, -0.20109708164787765], [3, -4.839806195049413, -39.92208742305105], [4, 4.18824810165454, 14.146847823548889]], [11.492663265706092, 16.36822198838621]], [[[1, 5.878492140223764, -19.955352450942357], [4, -7.059505455306587, -0.9740849280550585]], [19.628527845173146, 3.83678180657467]], [[[1, -11.150789592446378, -22.736641053247872], [4, -28.832815721158255, -3.9462962046291388]], [-19.841703647091965, 2.5113335861604362]], [[[1, 8.64427397916182, -20.286336970889053], [4, -5.036917727942285, -6.311739993868336]], [-5.946642674882207, -19.09548221169787]], [[[0, 7.151866679283043, -39.56103232616369], [1, 16.01535401373368, -3.780995345194027], [4, -3.04801331832137, 13.697362774960865]], [-5.946642674882207, -19.09548221169787]], [[[0, 12.872879480504395, -19.707592098123207], [1, 22.236710716903136, 16.331770792606406], [3, -4.841206109583004, -21.24604435851242], [4, 4.27111163223552, 32.25309748614184]], [-5.946642674882207, -19.09548221169787]]]
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
### Uncomment the following three lines for test case 2 and compare to the values above ###
mu_2 = slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_2, 20)
print_all(poses, landmarks)
# Here is the data and estimated outputs for test case 2
test_data2 = [[[[0, 26.543274387283322, -6.262538160312672], [3, 9.937396825799755, -9.128540360867689]], [18.92765331253674, -6.460955043986683]], [[[0, 7.706544739722961, -3.758467215445748], [1, 17.03954411948937, 31.705489938553438], [3, -11.61731288777497, -6.64964096716416]], [18.92765331253674, -6.460955043986683]], [[[0, -12.35130507136378, 2.585119104239249], [1, -2.563534536165313, 38.22159657838369], [3, -26.961236804740935, -0.4802312626141525]], [-11.167066095509824, 16.592065417497455]], [[[0, 1.4138633151721272, -13.912454837810632], [1, 8.087721200818589, 20.51845934354381], [3, -17.091723454402302, -16.521500551709707], [4, -7.414211721400232, 38.09191602674439]], [-11.167066095509824, 16.592065417497455]], [[[0, 12.886743222179561, -28.703968411636318], [1, 21.660953298391387, 3.4912891084614914], [3, -6.401401414569506, -32.321583037341625], [4, 5.034079343639034, 23.102207946092893]], [-11.167066095509824, 16.592065417497455]], [[[1, 31.126317672358578, -10.036784369535214], [2, -38.70878528420893, 7.4987265861424595], [4, 17.977218575473767, 6.150889254289742]], [-6.595520680493778, -18.88118393939265]], [[[1, 41.82460922922086, 7.847527392202475], [3, 15.711709540417502, -30.34633659912818]], [-6.595520680493778, -18.88118393939265]], [[[0, 40.18454208294434, -6.710999804403755], [3, 23.019508919299156, -10.12110867290604]], [-6.595520680493778, -18.88118393939265]], [[[3, 27.18579315312821, 8.067219022708391]], [-6.595520680493778, -18.88118393939265]], [[], [11.492663265706092, 16.36822198838621]], [[[3, 24.57154567653098, 13.461499960708197]], [11.492663265706092, 16.36822198838621]], [[[0, 31.61945290413707, 0.4272295085799329], [3, 16.97392299158991, -5.274596836133088]], [11.492663265706092, 16.36822198838621]], [[[0, 22.407381798735177, -18.03500068379259], [1, 29.642444125196995, 17.3794951934614], [3, 4.7969752441371645, -21.07505361639969], [4, 14.726069092569372, 32.75999422300078]], [11.492663265706092, 16.36822198838621]], [[[0, 10.705527984670137, -34.589764174299596], [1, 18.58772336795603, -0.20109708164787765], [3, -4.839806195049413, -39.92208742305105], [4, 4.18824810165454, 14.146847823548889]], [11.492663265706092, 16.36822198838621]], [[[1, 5.878492140223764, -19.955352450942357], [4, -7.059505455306587, -0.9740849280550585]], [19.628527845173146, 3.83678180657467]], [[[1, -11.150789592446378, -22.736641053247872], [4, -28.832815721158255, -3.9462962046291388]], [-19.841703647091965, 2.5113335861604362]], [[[1, 8.64427397916182, -20.286336970889053], [4, -5.036917727942285, -6.311739993868336]], [-5.946642674882207, -19.09548221169787]], [[[0, 7.151866679283043, -39.56103232616369], [1, 16.01535401373368, -3.780995345194027], [4, -3.04801331832137, 13.697362774960865]], [-5.946642674882207, -19.09548221169787]], [[[0, 12.872879480504395, -19.707592098123207], [1, 22.236710716903136, 16.331770792606406], [3, -4.841206109583004, -21.24604435851242], [4, 4.27111163223552, 32.25309748614184]], [-5.946642674882207, -19.09548221169787]]]
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
### Uncomment the following three lines for test case 2 and compare to the values above ###
mu_2 = slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_2, 20)
print_all(poses, landmarks)
Estimated Poses: [50.000, 50.000] [69.181, 45.665] [87.743, 39.703] [76.270, 56.311] [64.317, 72.176] [52.257, 88.154] [44.059, 69.401] [37.002, 49.918] [30.924, 30.955] [23.508, 11.419] [34.180, 27.133] [44.155, 43.846] [54.806, 60.920] [65.698, 78.546] [77.468, 95.626] [96.802, 98.821] [75.957, 99.971] [70.200, 81.181] [64.054, 61.723] [58.107, 42.628] Estimated Landmarks: [76.779, 42.887] [85.065, 77.438] [13.548, 95.652] [59.449, 39.595] [69.263, 94.240]
TODOs¶
- Create a new version of
slamin whichomegaonly keeps track of the latest robot pose (you do not need all of them to implementslamcorrectly).
See Udacity Artificial Intelligence for Robotics on how to implement online Graph SLAM. See also specific video.
- Add visualization code that creates a more realistic-looking display world
- Create a non-random maze of landmarks and see how your implementation of slam performs
- Display your robot world at every time step and stack these image frames to create a short video clip and to see how the robot localizes itself and builds up a model of the world over time
- Take a look at an implementation of slam that uses reinforcement learning and probabilistic motion models, at this Github link
Online SLAM¶
In [149]:
Copied!
## 1. Everytime we get a new pose we want to expand to grow the matrix by inserting something right behind the existing pose x_t
## 2. Take out sub-matrix omega_prime and sub vector xi_prime of the new pose x_t+1 and the landmarks
## 3. Calculate A, B from omega and C from xi
## 4. Reduced omega is obtained by omega = omega_prime - A^T B^-1 A
## 5. Reduced xi is obtained by xi = xi_prime A^T B^-1 C
## 1. Everytime we get a new pose we want to expand to grow the matrix by inserting something right behind the existing pose x_t
## 2. Take out sub-matrix omega_prime and sub vector xi_prime of the new pose x_t+1 and the landmarks
## 3. Calculate A, B from omega and C from xi
## 4. Reduced omega is obtained by omega = omega_prime - A^T B^-1 A
## 5. Reduced xi is obtained by xi = xi_prime A^T B^-1 C
In [150]:
Copied!
# ------------
#
# creates a new matrix from the existing matrix elements.
#
# Example:
# l = matrix([[ 1, 2, 3, 4, 5],
# [ 6, 7, 8, 9, 10],
# [11, 12, 13, 14, 15]])
#
# l.take([0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 3, 4],
# [11, 13, 14]]
#
#
# take is used to remove rows and columns from existing matrices
# list1/list2 define a sequence of rows/columns that shall be taken
# is no list2 is provided, then list2 is set to list1 (good for symmetric matrices)
#
def take(matrix, list1, list2 = []):
(m_rows, m_cols) = matrix.shape
if list2 == []:
list2 = list1
if len(list1) > m_rows or len(list2) > m_cols:
raise ValueError("list invalid in take()")
res = np.asmatrix(np.zeros((len(list1), len(list2))))
for i in range(len(list1)):
for j in range(len(list2)):
res[i, j] = matrix[list1[i], list2[j]]
return res
# ------------
#
# creates a new matrix from the existing matrix elements.
#
# Example:
# l = matrix([[1, 2, 3],
# [4, 5, 6]])
#
# l.expand(3, 5, [0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 0, 2, 3, 0],
# [0, 0, 0, 0, 0],
# [4, 0, 5, 6, 0]]
#
# expand is used to introduce new rows and columns into an existing matrix
# list1/list2 are the new indexes of row/columns in which the matrix
# elements are being mapped. Elements for rows and columns
# that are not listed in list1/list2
# will be initialized by 0.0.
#
def expand(matrix, rows, cols, list1, list2 = []):
(m_rows, m_cols) = matrix.shape
if list2 == []:
list2 = list1
if len(list1) > m_rows or len(list2) > m_cols:
raise ValueError("list invalid in expand()")
res = np.asmatrix(np.zeros((rows, cols)))
for i in range(len(list1)):
for j in range(len(list2)):
res[list1[i], list2[j]] = matrix[i,j]
return res
# ------------
#
# creates a new matrix from the existing matrix elements.
#
# Example:
# l = matrix([[ 1, 2, 3, 4, 5],
# [ 6, 7, 8, 9, 10],
# [11, 12, 13, 14, 15]])
#
# l.take([0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 3, 4],
# [11, 13, 14]]
#
#
# take is used to remove rows and columns from existing matrices
# list1/list2 define a sequence of rows/columns that shall be taken
# is no list2 is provided, then list2 is set to list1 (good for symmetric matrices)
#
def take(matrix, list1, list2 = []):
(m_rows, m_cols) = matrix.shape
if list2 == []:
list2 = list1
if len(list1) > m_rows or len(list2) > m_cols:
raise ValueError("list invalid in take()")
res = np.asmatrix(np.zeros((len(list1), len(list2))))
for i in range(len(list1)):
for j in range(len(list2)):
res[i, j] = matrix[list1[i], list2[j]]
return res
# ------------
#
# creates a new matrix from the existing matrix elements.
#
# Example:
# l = matrix([[1, 2, 3],
# [4, 5, 6]])
#
# l.expand(3, 5, [0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 0, 2, 3, 0],
# [0, 0, 0, 0, 0],
# [4, 0, 5, 6, 0]]
#
# expand is used to introduce new rows and columns into an existing matrix
# list1/list2 are the new indexes of row/columns in which the matrix
# elements are being mapped. Elements for rows and columns
# that are not listed in list1/list2
# will be initialized by 0.0.
#
def expand(matrix, rows, cols, list1, list2 = []):
(m_rows, m_cols) = matrix.shape
if list2 == []:
list2 = list1
if len(list1) > m_rows or len(list2) > m_cols:
raise ValueError("list invalid in expand()")
res = np.asmatrix(np.zeros((rows, cols)))
for i in range(len(list1)):
for j in range(len(list2)):
res[list1[i], list2[j]] = matrix[i,j]
return res
In [151]:
Copied!
l = np.matrix([[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15]])
take(l, [0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 3, 4],
# [11, 13, 14]]
l = np.matrix([[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15]])
take(l, [0, 2], [0, 2, 3])
#
# results in:
#
# [[1, 3, 4],
# [11, 13, 14]]
Out[151]:
matrix([[ 1., 3., 4.],
[ 11., 13., 14.]])
In [152]:
Copied!
l = np.matrix([[1, 2, 3],
[4, 5, 6]])
expand(l, 3, 5, [0, 2], [0, 2, 3])
# results in:
#
# [[1, 0, 2, 3, 0],
# [0, 0, 0, 0, 0],
# [4, 0, 5, 6, 0]]
l = np.matrix([[1, 2, 3],
[4, 5, 6]])
expand(l, 3, 5, [0, 2], [0, 2, 3])
# results in:
#
# [[1, 0, 2, 3, 0],
# [0, 0, 0, 0, 0],
# [4, 0, 5, 6, 0]]
Out[152]:
matrix([[ 1., 0., 2., 3., 0.],
[ 0., 0., 0., 0., 0.],
[ 4., 0., 5., 6., 0.]])
In [153]:
Copied!
def initialize_constraints_online(num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
# initialize constraint matrices with 0's
# 1 pose (x, y) and num_landmarks (x, y)
size = 2 * (1 + num_landmarks)
# add initial pose constraint
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
omega = np.asmatrix(np.zeros((size, size)))
omega[0,0] = 1
omega[1,1] = 1
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.asmatrix(np.zeros((size, 1)))
xi[0] = world_size/2
xi[1] = world_size/2
return omega, xi
def initialize_constraints_online(num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
# initialize constraint matrices with 0's
# 1 pose (x, y) and num_landmarks (x, y)
size = 2 * (1 + num_landmarks)
# add initial pose constraint
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
omega = np.asmatrix(np.zeros((size, size)))
omega[0,0] = 1
omega[1,1] = 1
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.asmatrix(np.zeros((size, 1)))
xi[0] = world_size/2
xi[1] = world_size/2
return omega, xi
In [154]:
Copied!
def construct_constraints_sense_online(omega, xi, measurement, measurement_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific measurement including its noise,
and returns constraint matrices, omega and xi.'''
landmark_index = measurement[0]
dx = measurement[1]
dy = measurement[2]
strength = 1.0 / measurement_noise
# incorporate sense constraint for x coordinate
x_idx = 0
lx_idx = 2 * (1 + landmark_index)
omega[x_idx,x_idx] += strength
omega[x_idx,lx_idx] += -strength
omega[lx_idx,x_idx] += -strength
omega[lx_idx,lx_idx] += strength
xi[x_idx] += -dx / measurement_noise
xi[lx_idx] += dx / measurement_noise
# incorporate sense constraint for y coordinate
y_idx = 1
ly_idx = 2 * (1 + landmark_index) + 1
omega[y_idx,y_idx] += strength
omega[y_idx,ly_idx] += -strength
omega[ly_idx,y_idx] += -strength
omega[ly_idx,ly_idx] += strength
xi[y_idx] += -dy / measurement_noise
xi[ly_idx] += dy / measurement_noise
return omega, xi
def construct_constraints_sense_online(omega, xi, measurement, measurement_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific measurement including its noise,
and returns constraint matrices, omega and xi.'''
landmark_index = measurement[0]
dx = measurement[1]
dy = measurement[2]
strength = 1.0 / measurement_noise
# incorporate sense constraint for x coordinate
x_idx = 0
lx_idx = 2 * (1 + landmark_index)
omega[x_idx,x_idx] += strength
omega[x_idx,lx_idx] += -strength
omega[lx_idx,x_idx] += -strength
omega[lx_idx,lx_idx] += strength
xi[x_idx] += -dx / measurement_noise
xi[lx_idx] += dx / measurement_noise
# incorporate sense constraint for y coordinate
y_idx = 1
ly_idx = 2 * (1 + landmark_index) + 1
omega[y_idx,y_idx] += strength
omega[y_idx,ly_idx] += -strength
omega[ly_idx,y_idx] += -strength
omega[ly_idx,ly_idx] += strength
xi[y_idx] += -dy / measurement_noise
xi[ly_idx] += dy / measurement_noise
return omega, xi
In [155]:
Copied!
def construct_constraints_move_online(omega, xi, motion, motion_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific motion including its noise,
and returns constraint matrices, omega and xi.'''
dx = motion[0]
dy = motion[1]
strength = 1.0 / motion_noise #1 #/motion_noise
# incorporate motion constraint for x coordinate
x0 = 0
x1 = x0 + 2
omega[x0,x0] += strength
omega[x0,x1] += -strength
omega[x1,x0] += -strength
omega[x1,x1] += strength
xi[x0] += -dx / motion_noise
xi[x1] += dx / motion_noise
# incorporate motion constraint for y coordinate
y0 = 1
y1 = y0 + 2
omega[y0,y0] += strength
omega[y0,y1] += -strength
omega[y1,y0] += -strength
omega[y1,y1] += strength
xi[y0] += -dy / motion_noise
xi[y1] += dy / motion_noise
return omega, xi
def construct_constraints_move_online(omega, xi, motion, motion_noise):
''' This function takes in a number of time steps and landmarks for the new constraint matrices, and a specific motion including its noise,
and returns constraint matrices, omega and xi.'''
dx = motion[0]
dy = motion[1]
strength = 1.0 / motion_noise #1 #/motion_noise
# incorporate motion constraint for x coordinate
x0 = 0
x1 = x0 + 2
omega[x0,x0] += strength
omega[x0,x1] += -strength
omega[x1,x0] += -strength
omega[x1,x1] += strength
xi[x0] += -dx / motion_noise
xi[x1] += dx / motion_noise
# incorporate motion constraint for y coordinate
y0 = 1
y1 = y0 + 2
omega[y0,y0] += strength
omega[y0,y1] += -strength
omega[y1,y0] += -strength
omega[y1,y1] += strength
xi[y0] += -dy / motion_noise
xi[y1] += dy / motion_noise
return omega, xi
In [156]:
Copied!
def online_slam_step(data, time_step, omega, xi, motion_noise, measurement_noise):
k = time_step
measurements = data[k][0]
motion = data[k][1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measurement in measurements:
omega, xi = construct_constraints_sense_online(omega, xi, measurement, measurement_noise)
# expand the information matrix and vector by one new position
size = 2 * (1 + num_landmarks)
list1 = [0, 1] + list(range(4, size+2))
omega = expand(omega, size+2, size+2, list1, list1)
xi = expand(xi, size+2, 1, list1, [0])
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
omega, xi = construct_constraints_move_online(omega, xi, motion, motion_noise)
# factor out the previous pose
newlist = list(range(2, omega.shape[0]))
a = take(omega, [0, 1], newlist)
b = take(omega, [0, 1])
c = take(xi, [0, 1], [0])
#print(a.shape)
#print(b.shape)
#print(c.shape)
#print(np.linalg.inv(b).shape)
omega = take(omega, newlist) - a.transpose() * np.linalg.inv(b) * a
xi = take(xi, newlist, [0]) - a.transpose() * np.linalg.inv(b) * c
return omega, xi
def online_slam_step(data, time_step, omega, xi, motion_noise, measurement_noise):
k = time_step
measurements = data[k][0]
motion = data[k][1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measurement in measurements:
omega, xi = construct_constraints_sense_online(omega, xi, measurement, measurement_noise)
# expand the information matrix and vector by one new position
size = 2 * (1 + num_landmarks)
list1 = [0, 1] + list(range(4, size+2))
omega = expand(omega, size+2, size+2, list1, list1)
xi = expand(xi, size+2, 1, list1, [0])
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
omega, xi = construct_constraints_move_online(omega, xi, motion, motion_noise)
# factor out the previous pose
newlist = list(range(2, omega.shape[0]))
a = take(omega, [0, 1], newlist)
b = take(omega, [0, 1])
c = take(xi, [0, 1], [0])
#print(a.shape)
#print(b.shape)
#print(c.shape)
#print(np.linalg.inv(b).shape)
omega = take(omega, newlist) - a.transpose() * np.linalg.inv(b) * a
xi = take(xi, newlist, [0]) - a.transpose() * np.linalg.inv(b) * c
return omega, xi
In [157]:
Copied!
def compute_pose_and_landmarks(omega, xi):
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
try:
omega_inv = np.linalg.inv(omega)
except:
print("Computing (Moore-Penrose) pseudo-inverse")
omega_inv = np.linalg.pinv(omega)
mu = omega_inv*xi
return mu
def compute_pose_and_landmarks(omega, xi):
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
try:
omega_inv = np.linalg.inv(omega)
except:
print("Computing (Moore-Penrose) pseudo-inverse")
omega_inv = np.linalg.pinv(omega)
mu = omega_inv*xi
return mu
In [158]:
Copied!
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def online_slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
omega, xi = initialize_constraints_online(num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
for time_step in range(len(data)):
omega, xi = online_slam_step(data, time_step, omega, xi, motion_noise, measurement_noise)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(omega, xi)
return mu # return `mu`
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def online_slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
omega, xi = initialize_constraints_online(num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
for time_step in range(len(data)):
omega, xi = online_slam_step(data, time_step, omega, xi, motion_noise, measurement_noise)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(omega, xi)
return mu # return `mu`
In [159]:
Copied!
# call your implementation of slam, passing in the necessary parameters
mu = online_slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# call your implementation of slam, passing in the necessary parameters
mu = online_slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
In [160]:
Copied!
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
pose, landmarks = get_pose_landmarks_online(mu)
print_all_online(pose, landmarks)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
pose, landmarks = get_pose_landmarks_online(mu)
print_all_online(pose, landmarks)
Estimated Pose: [82.204, 5.921] Estimated Landmarks: [18.364, 89.130] [69.980, 86.949] [91.585, 5.242] [51.569, 26.748] [63.195, 51.718]
In [161]:
Copied!
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1 = online_slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
pose_1, landmarks_1 = get_pose_landmarks_online(mu_1)
print_all_online(pose_1, landmarks_1)
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1 = online_slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
pose_1, landmarks_1 = get_pose_landmarks_online(mu_1)
print_all_online(pose_1, landmarks_1)
Estimated Pose: [37.416, 22.317] Estimated Landmarks: [82.956, 13.539] [70.495, 74.141] [36.740, 61.281] [18.698, 66.060] [20.635, 16.875]
In [162]:
Copied!
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
pose_2, landmarks_2 = get_pose_landmarks_online(mu_2)
print_all_online(pose_2, landmarks_2)
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
pose_2, landmarks_2 = get_pose_landmarks_online(mu_2)
print_all_online(pose_2, landmarks_2)
Estimated Pose: [58.107, 42.628] Estimated Landmarks: [76.779, 42.887] [85.065, 77.438] [13.548, 95.652] [59.449, 39.595] [69.263, 94.240]
In [163]:
Copied!
from matplotlib.legend_handler import HandlerBase
from matplotlib.legend_handler import HandlerLine2D, HandlerTuple
from helpers import TextHandlerA
from matplotlib.text import Text
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
class OnlineSLAM:
def __init__(self, ax, data, robot=None, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0):
self.ax = ax
self.data = data
self.robot = robot
self.landmarks = None
if robot is not None:
self.robot.path = np.array(robot.path)
self.landmarks = self.robot.landmarks
print(self.landmarks)
self.motion_noise = motion_noise
self.measurement_noise = measurement_noise
# using seaborn, set background grid to gray
sns.set_style("dark")
# Plot grid of values
world_grid = np.zeros((world_size+1, world_size+1))
# Set minor axes in between the labels
cols = world_size+1
rows = world_size+1
self.ax.set_xticks([x for x in range(1,cols)],minor=True)
self.ax.set_yticks([y for y in range(1,rows)],minor=True)
# Plot grid on minor axes in gray (width = 1)
plt.grid(which='minor',ls='-',lw=1, color='white')
# Plot grid on major axes in larger width
plt.grid(which='major',ls='-',lw=2, color='white')
plt.xlim([0, world_size])
plt.ylim([0, world_size])
def init(self):
self.robot_gt_poses = []
self.robot_gt_path = []
if self.robot is not None:
# Robot and its path
self.robot_gt_path, = self.ax.plot(self.robot.path[:,0], self.robot.path[:,1], color='g', alpha=0.3)
for i, pose in enumerate(self.robot.path):
self.robot_gt_circle = plt.Circle((pose[0], pose[1]), radius=1, color='g', alpha=0.3)
self.robot_gt_poses.append(self.ax.add_patch(self.robot_gt_circle))
label = ax.annotate(f"{i}", xy=(pose[0], pose[1]), fontsize=10, ha="center", va='center')
# Landmarks (ground truth)
self.landmarks_gt = []
if self.landmarks is not None:
size = 1
for location in landmarks:
#print(location)
landmark_gt_rect = plt.Rectangle([location[0]-size, location[1]-size], 2*size, 2*size, lw=0.5, color='b', alpha=0.1)
self.landmarks_gt.append(self.ax.add_patch(landmark_gt_rect))
artists = self.robot_gt_poses + [self.robot_gt_path] + self.landmarks_gt
return artists
def __call__(self, frame):
if frame == 0:
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
self.omega, self.xi = initialize_constraints_online(num_landmarks, world_size)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(self.omega, self.xi)
position, landmarks = get_pose_landmarks_online(mu)
self.robot_est_text = ax.text(position[0], position[1], 'o', ha='center', va='center', color='r', fontsize=30)
self.landmarks_est_text = []
self.laser_scans = []
for i, landmark in enumerate(landmarks):
self.landmarks_est_text.append(self.ax.text(landmark[0], landmark[1], 'x', ha='center', va='center', color='purple', fontsize=20))
# Draw laser from robot to observed landmarks
#laser_scan, = self.ax.plot([position[0], landmark[0]], [position[1], landmark[1]], color='k', linestyle='dashed')
#self.laser_scans.append(laser_scan)
for i, landmark in enumerate(self.robot.landmarks):
# Draw laser from robot to observed landmarks
dx = landmark[0] - position[0]
dy = landmark[1] - position[1]
if abs(dx) <= self.robot.measurement_range and abs(dy) <= self.robot.measurement_range:
laser_scan, = self.ax.plot([position[0], landmark[0]], [position[1], landmark[1]], color='k', linestyle='dashed')
else:
laser_scan, = self.ax.plot([], [], color='k', linestyle='dashed')
self.laser_scans.append(laser_scan)
else:
time_step = frame - 1
## Iterate through each time step in the data
## get all the motion and measurement data as you iterate
self.omega, self.xi = online_slam_step(self.data, time_step, self.omega, self.xi, self.motion_noise, self.measurement_noise)
#print(self.omega)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(self.omega, self.xi)
position, landmarks = get_pose_landmarks_online(mu)
# Create an 'o' character that represents the robot
# ha = horizontal alignment, va = vertical
#ax.text(position[0], position[1], 'o', ha='center', va='center', color='r', fontsize=30)
self.robot_est_text.set_x(position[0])
self.robot_est_text.set_y(position[1])
# Draw landmarks if they exists
if(landmarks is not None):
# loop through all path indices and draw a dot (unless it's at the car's location)
for i, landmark in enumerate(landmarks):
if(landmark != position):
#ax.text(pos[0], pos[1], 'x', ha='center', va='center', color='purple', fontsize=20)
self.landmarks_est_text[i].set_x(landmark[0])
self.landmarks_est_text[i].set_y(landmark[1])
for i, landmark in enumerate(self.robot.landmarks):
# Draw laser from robot to observed landmarks
dx = landmark[0] - position[0]
dy = landmark[1] - position[1]
if abs(dx) <= self.robot.measurement_range and abs(dy) <= self.robot.measurement_range:
self.laser_scans[i].set_data([position[0], landmark[0]], [position[1], landmark[1]])
else:
self.laser_scans[i].set_data([], [])
print(self.robot_est_text, len(landmarks))
self.ax.legend([(self.robot_gt_circle, self.robot_gt_path), self.robot_est_text, self.landmarks_gt[0], self.landmarks_est_text[0], self.laser_scans[0]],
['Robot ground truth path', 'Robot final pose', 'Landmark ground truth', 'Landmark estimates', 'Laser scans'],
numpoints=1, handler_map={tuple: HandlerTuple(ndivide=None), Text: TextHandlerA()})
artists = [self.robot_est_text] + self.landmarks_est_text + self.laser_scans
return artists
from matplotlib.legend_handler import HandlerBase
from matplotlib.legend_handler import HandlerLine2D, HandlerTuple
from helpers import TextHandlerA
from matplotlib.text import Text
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
class OnlineSLAM:
def __init__(self, ax, data, robot=None, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0):
self.ax = ax
self.data = data
self.robot = robot
self.landmarks = None
if robot is not None:
self.robot.path = np.array(robot.path)
self.landmarks = self.robot.landmarks
print(self.landmarks)
self.motion_noise = motion_noise
self.measurement_noise = measurement_noise
# using seaborn, set background grid to gray
sns.set_style("dark")
# Plot grid of values
world_grid = np.zeros((world_size+1, world_size+1))
# Set minor axes in between the labels
cols = world_size+1
rows = world_size+1
self.ax.set_xticks([x for x in range(1,cols)],minor=True)
self.ax.set_yticks([y for y in range(1,rows)],minor=True)
# Plot grid on minor axes in gray (width = 1)
plt.grid(which='minor',ls='-',lw=1, color='white')
# Plot grid on major axes in larger width
plt.grid(which='major',ls='-',lw=2, color='white')
plt.xlim([0, world_size])
plt.ylim([0, world_size])
def init(self):
self.robot_gt_poses = []
self.robot_gt_path = []
if self.robot is not None:
# Robot and its path
self.robot_gt_path, = self.ax.plot(self.robot.path[:,0], self.robot.path[:,1], color='g', alpha=0.3)
for i, pose in enumerate(self.robot.path):
self.robot_gt_circle = plt.Circle((pose[0], pose[1]), radius=1, color='g', alpha=0.3)
self.robot_gt_poses.append(self.ax.add_patch(self.robot_gt_circle))
label = ax.annotate(f"{i}", xy=(pose[0], pose[1]), fontsize=10, ha="center", va='center')
# Landmarks (ground truth)
self.landmarks_gt = []
if self.landmarks is not None:
size = 1
for location in landmarks:
#print(location)
landmark_gt_rect = plt.Rectangle([location[0]-size, location[1]-size], 2*size, 2*size, lw=0.5, color='b', alpha=0.1)
self.landmarks_gt.append(self.ax.add_patch(landmark_gt_rect))
artists = self.robot_gt_poses + [self.robot_gt_path] + self.landmarks_gt
return artists
def __call__(self, frame):
if frame == 0:
## TODO: Use your initilization to create constraint matrices, omega and xi
# initialize the constraints
self.omega, self.xi = initialize_constraints_online(num_landmarks, world_size)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(self.omega, self.xi)
position, landmarks = get_pose_landmarks_online(mu)
self.robot_est_text = ax.text(position[0], position[1], 'o', ha='center', va='center', color='r', fontsize=30)
self.landmarks_est_text = []
self.laser_scans = []
for i, landmark in enumerate(landmarks):
self.landmarks_est_text.append(self.ax.text(landmark[0], landmark[1], 'x', ha='center', va='center', color='purple', fontsize=20))
# Draw laser from robot to observed landmarks
#laser_scan, = self.ax.plot([position[0], landmark[0]], [position[1], landmark[1]], color='k', linestyle='dashed')
#self.laser_scans.append(laser_scan)
for i, landmark in enumerate(self.robot.landmarks):
# Draw laser from robot to observed landmarks
dx = landmark[0] - position[0]
dy = landmark[1] - position[1]
if abs(dx) <= self.robot.measurement_range and abs(dy) <= self.robot.measurement_range:
laser_scan, = self.ax.plot([position[0], landmark[0]], [position[1], landmark[1]], color='k', linestyle='dashed')
else:
laser_scan, = self.ax.plot([], [], color='k', linestyle='dashed')
self.laser_scans.append(laser_scan)
else:
time_step = frame - 1
## Iterate through each time step in the data
## get all the motion and measurement data as you iterate
self.omega, self.xi = online_slam_step(self.data, time_step, self.omega, self.xi, self.motion_noise, self.measurement_noise)
#print(self.omega)
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
mu = compute_pose_and_landmarks(self.omega, self.xi)
position, landmarks = get_pose_landmarks_online(mu)
# Create an 'o' character that represents the robot
# ha = horizontal alignment, va = vertical
#ax.text(position[0], position[1], 'o', ha='center', va='center', color='r', fontsize=30)
self.robot_est_text.set_x(position[0])
self.robot_est_text.set_y(position[1])
# Draw landmarks if they exists
if(landmarks is not None):
# loop through all path indices and draw a dot (unless it's at the car's location)
for i, landmark in enumerate(landmarks):
if(landmark != position):
#ax.text(pos[0], pos[1], 'x', ha='center', va='center', color='purple', fontsize=20)
self.landmarks_est_text[i].set_x(landmark[0])
self.landmarks_est_text[i].set_y(landmark[1])
for i, landmark in enumerate(self.robot.landmarks):
# Draw laser from robot to observed landmarks
dx = landmark[0] - position[0]
dy = landmark[1] - position[1]
if abs(dx) <= self.robot.measurement_range and abs(dy) <= self.robot.measurement_range:
self.laser_scans[i].set_data([position[0], landmark[0]], [position[1], landmark[1]])
else:
self.laser_scans[i].set_data([], [])
print(self.robot_est_text, len(landmarks))
self.ax.legend([(self.robot_gt_circle, self.robot_gt_path), self.robot_est_text, self.landmarks_gt[0], self.landmarks_est_text[0], self.laser_scans[0]],
['Robot ground truth path', 'Robot final pose', 'Landmark ground truth', 'Landmark estimates', 'Laser scans'],
numpoints=1, handler_map={tuple: HandlerTuple(ndivide=None), Text: TextHandlerA()})
artists = [self.robot_est_text] + self.landmarks_est_text + self.laser_scans
return artists
In [164]:
Copied!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot=robot, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0)
plt.close()
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot=robot, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0)
plt.close()
[[18, 89], [69, 87], [90, 4], [50, 26], [62, 51]]
In [165]:
Copied!
from matplotlib.animation import FuncAnimation
from matplotlib.animation import FuncAnimation
In [166]:
Copied!
anim_html = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
anim_html = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
In [167]:
Copied!
from IPython.display import HTML
HTML(anim_html.to_html5_video())
from IPython.display import HTML
HTML(anim_html.to_html5_video())
Computing (Moore-Penrose) pseudo-inverse Text(50,50,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(49.6242,69.9965,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(49.2099,90.0445,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(64.8832,78.6377,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(81.2858,65.7794,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(97.7488,52.8012,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(80.2032,42.0594,'o') 5 Text(63.2944,30.2655,'o') 5 Text(45.4809,18.0168,'o') 5 Text(27.9926,8.06578,'o') 5 Text(32.1712,28.9251,'o') 5 Text(36.7148,48.5267,'o') 5 Text(41.8487,66.9221,'o') 5 Text(49.0019,85.2264,'o') 5 Text(31.3999,94.0156,'o') 5 Text(40.5245,75.8164,'o') 5 Text(49.9822,59.7349,'o') 5 Text(61.2975,42.9729,'o') 5 Text(71.1077,24.2067,'o') 5 Text(82.2039,5.92124,'o') 5
Out[167]:
In [168]:
Copied!
plt.rcParams["animation.html"]
plt.rcParams["animation.html"]
Out[168]:
'jshtml'
In [169]:
Copied!
# https://stackoverflow.com/a/47138474/2137370
%matplotlib inline
plt.rcParams["animation.html"] = "jshtml"
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot=robot, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0)
plt.close()
# https://stackoverflow.com/a/47138474/2137370
%matplotlib inline
plt.rcParams["animation.html"] = "jshtml"
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot=robot, num_landmarks=5, world_size=100, motion_noise=2.0, measurement_noise=2.0)
plt.close()
[[18, 89], [69, 87], [90, 4], [50, 26], [62, 51]]
In [170]:
Copied!
anim = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
anim
anim = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
anim
Computing (Moore-Penrose) pseudo-inverse Text(50,50,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(49.6242,69.9965,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(49.2099,90.0445,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(64.8832,78.6377,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(81.2858,65.7794,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(97.7488,52.8012,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(80.2032,42.0594,'o') 5 Text(63.2944,30.2655,'o') 5 Text(45.4809,18.0168,'o') 5 Text(27.9926,8.06578,'o') 5 Text(32.1712,28.9251,'o') 5 Text(36.7148,48.5267,'o') 5 Text(41.8487,66.9221,'o') 5 Text(49.0019,85.2264,'o') 5 Text(31.3999,94.0156,'o') 5 Text(40.5245,75.8164,'o') 5 Text(49.9822,59.7349,'o') 5 Text(61.2975,42.9729,'o') 5 Text(71.1077,24.2067,'o') 5 Text(82.2039,5.92124,'o') 5
Out[170]:
Create a non-random maze of landmarks and see how your implementation of slam performs¶
In [177]:
Copied!
%load_ext autoreload
%autoreload 2
%load_ext autoreload
%autoreload 2
The autoreload extension is already loaded. To reload it, use: %reload_ext autoreload
In [178]:
Copied!
from robot_class import robot
num_landmarks = 5
r = robot()
r.make_deterministic_landmarks(num_landmarks)
r.landmarks
from robot_class import robot
num_landmarks = 5
r = robot()
r.make_deterministic_landmarks(num_landmarks)
r.landmarks
Out[178]:
[[10.0, 10.0], [10.0, 50.0], [10.0, 90.0], [90.0, 10.0], [90.0, 50.0]]
In [179]:
Copied!
from robot_class import robot
from math import *
import random
# --------
# this routine makes the robot data
# the data is a list of measurements and movements: [measurements, [dx, dy]]
# collected over a specified number of time steps, N
#
def make_non_random_data(N, num_landmarks, world_size, measurement_range, motion_noise,
measurement_noise, distance):
# check that data has been made
try:
check_for_data(num_landmarks, world_size, measurement_range, motion_noise, measurement_noise)
except ValueError:
print('Error: You must implement the sense function in robot_class.py.')
return []
complete = False
r = robot(world_size, measurement_range, motion_noise, measurement_noise)
r.make_deterministic_landmarks(num_landmarks)
while not complete:
data = []
seen = [False for row in range(num_landmarks)]
# guess an initial motion
#orientation = random.random() * 2.0 * pi
orientation = 0 * 2.0 * pi
dx = cos(orientation) * distance
dy = sin(orientation) * distance
for k in range(N-1):
# collect sensor measurements in a list, Z
Z = r.sense()
# check off all landmarks that were observed
for i in range(len(Z)):
seen[Z[i][0]] = True
# move
#o = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
#o = o + o
while not r.move(dx, dy):
# if we'd be leaving the robot world, pick instead a new direction
orientation = random.random() * 2.0 * pi
#orientation = o[k] * 2.0 * pi
dx = cos(orientation) * distance
dy = sin(orientation) * distance
# collect/memorize all sensor and motion data
data.append([Z, [dx, dy]])
# we are done when all landmarks were observed; otherwise re-run
complete = (sum(seen) == num_landmarks)
print(' ')
print('Landmarks: ', r.landmarks)
print(r)
return data, r
def check_for_data(num_landmarks, world_size, measurement_range, motion_noise, measurement_noise):
# make robot and landmarks
r = robot(world_size, measurement_range, motion_noise, measurement_noise)
r.make_deterministic_landmarks(num_landmarks)
# check that sense has been implemented/data has been made
test_Z = r.sense()
if(test_Z is None):
raise ValueError
from robot_class import robot
from math import *
import random
# --------
# this routine makes the robot data
# the data is a list of measurements and movements: [measurements, [dx, dy]]
# collected over a specified number of time steps, N
#
def make_non_random_data(N, num_landmarks, world_size, measurement_range, motion_noise,
measurement_noise, distance):
# check that data has been made
try:
check_for_data(num_landmarks, world_size, measurement_range, motion_noise, measurement_noise)
except ValueError:
print('Error: You must implement the sense function in robot_class.py.')
return []
complete = False
r = robot(world_size, measurement_range, motion_noise, measurement_noise)
r.make_deterministic_landmarks(num_landmarks)
while not complete:
data = []
seen = [False for row in range(num_landmarks)]
# guess an initial motion
#orientation = random.random() * 2.0 * pi
orientation = 0 * 2.0 * pi
dx = cos(orientation) * distance
dy = sin(orientation) * distance
for k in range(N-1):
# collect sensor measurements in a list, Z
Z = r.sense()
# check off all landmarks that were observed
for i in range(len(Z)):
seen[Z[i][0]] = True
# move
#o = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
#o = o + o
while not r.move(dx, dy):
# if we'd be leaving the robot world, pick instead a new direction
orientation = random.random() * 2.0 * pi
#orientation = o[k] * 2.0 * pi
dx = cos(orientation) * distance
dy = sin(orientation) * distance
# collect/memorize all sensor and motion data
data.append([Z, [dx, dy]])
# we are done when all landmarks were observed; otherwise re-run
complete = (sum(seen) == num_landmarks)
print(' ')
print('Landmarks: ', r.landmarks)
print(r)
return data, r
def check_for_data(num_landmarks, world_size, measurement_range, motion_noise, measurement_noise):
# make robot and landmarks
r = robot(world_size, measurement_range, motion_noise, measurement_noise)
r.make_deterministic_landmarks(num_landmarks)
# check that sense has been implemented/data has been made
test_Z = r.sense()
if(test_Z is None):
raise ValueError
In [180]:
Copied!
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 40.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data, robot = make_non_random_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 40.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data, robot = make_non_random_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
Landmarks: [[10.0, 10.0], [10.0, 50.0], [10.0, 90.0], [90.0, 10.0], [90.0, 50.0]] Robot: [x=52.52432 y=71.44035]
In [181]:
Copied!
# call your implementation of slam, passing in the necessary parameters
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
# call your implementation of slam, passing in the necessary parameters
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
Estimated Poses: [50.000, 50.000] [69.528, 49.516] [90.579, 49.646] [70.996, 55.000] [53.275, 58.891] [35.255, 62.487] [15.488, 66.598] [8.519, 47.615] [1.766, 28.629] [22.054, 31.112] [41.874, 33.695] [61.903, 37.520] [80.723, 42.557] [99.481, 45.778] [97.800, 25.893] [97.134, 5.985] [84.699, 23.041] [73.154, 39.108] [61.523, 55.916] [50.098, 72.332] Estimated Landmarks: [10.707, 10.007] [10.406, 51.815] [9.920, 90.045] [90.765, 11.672] [90.054, 51.219]
In [182]:
Copied!
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
print('True last pose: ', robot.path[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
display_world_extended(int(world_size), poses[-1], landmarks, robot)
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
print('True last pose: ', robot.path[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
display_world_extended(int(world_size), poses[-1], landmarks, robot)
Last pose: (50.09830494951987, 72.33173953448954) True last pose: [52.524320896194645, 71.44034682637752]
Online SLAM¶
In [183]:
Copied!
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot, num_landmarks, int(world_size), motion_noise, measurement_noise)
plt.close()
# define figure size
plt.rcParams["figure.figsize"] = (10,10)
fig, ax = plt.subplots()
# data, N, num_landmarks, world_size, motion_noise, measurement_noise
# mu_2 = online_slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
ud = OnlineSLAM(ax, data, robot, num_landmarks, int(world_size), motion_noise, measurement_noise)
plt.close()
[[10.0, 10.0], [10.0, 50.0], [10.0, 90.0], [90.0, 10.0], [90.0, 50.0]]
In [184]:
Copied!
anim_html = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
anim_html = FuncAnimation(fig, ud, init_func=ud.init, frames=len(data)+1, interval=1000, blit=True)
In [185]:
Copied!
from IPython.display import HTML
HTML(anim_html.to_html5_video())
from IPython.display import HTML
HTML(anim_html.to_html5_video())
Computing (Moore-Penrose) pseudo-inverse Text(50,50,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(70,50,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(89.2718,49.4945,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(70.5281,53.2742,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(49.7275,59.1074,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(32.0338,63.1119,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(15.6308,66.4505,'o') 5 Computing (Moore-Penrose) pseudo-inverse Text(9.37764,47.6468,'o') 5 Text(2.98157,28.9266,'o') 5 Text(20.8408,33.4502,'o') 5 Text(41.0721,35.8401,'o') 5 Text(61.0277,38.0193,'o') 5 Text(81.5409,41.3692,'o') 5 Text(100.435,46.8982,'o') 5 Text(98.7807,25.582,'o') 5 Text(96.7986,5.8083,'o') 5 Text(86.2374,21.8918,'o') 5 Text(73.2503,39.4892,'o') 5 Text(61.8124,55.366,'o') 5 Text(50.0983,72.3317,'o') 5
Out[185]: